![[til]처음시작하는 머신러닝 11장](https://taewanmerepo.github.io/2018/08/til20180819/list.jpg)
![[til]처음시작하는 머신러닝 11장](https://taewanmerepo.github.io/2018/08/til20180819/list.jpg)
![[til]처음시작하는 머신러닝 6-9장](https://taewanmerepo.github.io/2018/08/til20180919/list.jpg)
[til]처음시작하는 머신러닝 6-9장
7장 추천 유사도 Jaccard similarity coefficient: 두 집합의 원소의 유사도 개념 두 집합 A, B $\frac{|A \cap B|}{|A \cup B|} $ 두 집합의 교집합 원소 수와 합집합 원소 수의 비율 특징 희소 벡터로 구성된 데이터에 대한 집단 비교에 유용함 Cosine Similarity: 방향 $sim(X, Y) = \frac{X \cdot Y}{||X||\ ||Y||}$ X, Y 벡터 ......
![[til]처음시작하는 머신러닝 4-5장](https://taewanmerepo.github.io/2018/08/til20180817/list.jpg)
[til]처음시작하는 머신러닝 4-5장
4. 군집화 Euclidean Distance $$ d(x, y) = \sqrt{\sum^n_{i=1}(x_i-y_i)^2} = ||X-Y|| $$
$$ Squared Euclidean Distance = \sum^n_{i=1}(x_i-y_i)^2=||X-Y||^2_2 $$
군집화 유형 중심기반 군집화 k-means clustering k-medians clustering k-modes clustering 계층적 군집화 밀도기반 군집화 ......
![[til]처음시작하는 머신러닝 2-3장](https://taewanmerepo.github.io/2018/08/til20180815/list2.jpg)
[til]처음시작하는 머신러닝 2-3장
2장. 주요 개념 Topic Model Loss Function Optimization Model Evaluation Model 모델이란 데이터에 대한 가정(Hypothesis)의 총합
통계학에서는 Hypothesis를 Belief라고 함 단순(간단) 모델
데이터의 단순성을 가정 이해하기 쉬운 결과 학습 용이 복잡한 데이터를 학습하기 어려움(표현력 제약) 복잡한 모델
가정이 없음 이해하기 어려운 결과 학습이 복잡 새로운 데이터 ......
![[til]처음시작하는 머신러닝 1장](https://taewanmerepo.github.io/2018/08/til20180813/list.jpg)
[til]처음시작하는 머신러닝 1장
머신러닝 정의 머신러닝이란? 데이터를 이용하여 명시적으로 정의하지 않은 패턴을 컴퓨터로 학습하여 결과를 만들어내는 학문 분야
1959, 아서 사무엘(Arthur Lee Samuel) 머신러닝 구성 요소 Data Pattern Recognition Computing 머시러닝 관련 학문 수학 - 행렬 - 선형대수: 행렬분해 - 확률: 조건부 확률 통계학: 데이터에서 패턴을 찾아내는 학문 - 정규 분포, 가우스분포, 상관관계 컴퓨터 공학 ......

머신러닝을 위한 기초 수학
시그마, 파이, 미분, 편미분, 합성함수, 백터 및 행렬, 기하벡터, 지수, 대수에 대하여 요점 정리합니다.
Sigma & Phi 1 부터 100까지 합산 $$ \sum_{i=1}^{100}i $$
몇시적으로 마지막 값을 모르는 합산 $$ \sum_{i=1}^{n}i $$
집합 합산 $$ G = {2, 3, 6, 8, 10} \\
\sum_{g \in G}g $$
모든 것을 곱함 (1~100) $$ 1 \cdot 2 \cdot 3 \cdot 4 \cdot \cdot \cdot 99 \cdot 100 \\
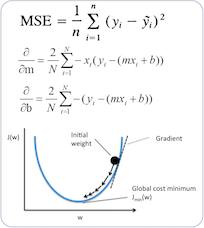
비용 함수 MSE를 미분하여 경사하강법 유도
2장. 지도학습 지도학습 “Input/Label”로 구성된 사례 데이터를 이용하여 ML 모델을 학습 최종 목표: 새로운 데이터를 정확하게 에측하는 것 유형: 회귀 & 분류 2.1 분류와 회귀 그림 1: 지도학습 요약 2.2 일반화, 과대적합, 과소적합 Generalization: 일반화 새로운 데이터에 정확한 예측을 제공하는 모델의 역량 모델이 복잡해 지면 학습셋에만 정확한 예측 제공 학습데이터에만 ......
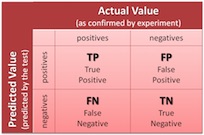
Classification 성능 matrix
분류 평가 기준 그림 1: Accuracy: 정확도 정확도: 전체 데이터 중에서 정확하게 분류한 비율 그림 2: Precision: 정밀도 정밀도: 양성의 예측 중에서 진짜로 양성인 비율 양성의 품질을 중요시 하는 경향 그림 3: Recall 재현율: 실제 양성 중에서 양성으로 분류한 비율 원본의 상태를 중시하는 경향 ROC Curve 그림 4: Recall & FPR 진짜 양성 비율: 양성관측한 것이 양성 가짜 음성 비율: 양성으로 예측, 음성
![[til]기초 확률&통계#8: 확률 변수, 확률 분포, 이산확률 분포](https://taewanmerepo.github.io/2018/08/til20180806/list.jpg)
[til]기초 확률&통계#8: 확률 변수, 확률 분포, 이산확률 분포
01. 확률 변수, 확률 분포 확률변수, 확률 분포는 함수다.
Sample Space는 시행에서 얻어지는 모든 결과의 집합. Sample Space의 모든 원소를 실수로 대응하는 함수: 확률 변수 확률 변수로 얻어진 실수를 확률값으로 변화하는 함수: 확률 분포 확률 변수와 확률 분포를 이용하여 시행의 결과를 실수로 변환할 수 있고, 발생 확률로 변환할 수 있다. 그림 1: 확률 변수와 확률 분포는 함수다 최종 확률분포표로 제시 02.

가우스가 들려주는 근삿값과 오차 이야기
오차의 역사 천문학에서는 특정 관측이 다양한 관측치로 측정되는 문제가 있습니다. 이 중에서 어떤 것이 정확한 관측인지를 알기 위해서 오차를 없애는 방법을 학문적으로 연구하기 시작했습니다.
갈릴레오 갈렐리이는 참값(Truth Value)에는 많은 관측치가 존재하지만 먼 관측치는 드물다. 관측치의 빈도를 그래프로 그리면 종 모양이 된다고 했고, 이 개념은 후에 가오스 분포로 증명되었습니다.
그림 1: 관측치 빈도 그래프: 종모양 => 가우스 ......
![[til]기초 확률&통계#8: 사건의 독립과 종속](https://taewanmerepo.github.io/2018/08/til20180803/list.jpg)
[til]기초 확률&통계#8: 사건의 독립과 종속
01. 사건의 독립과 종속 예제 10개의 제비뽑기가 있음, 당첨제베는 2개, 철수와 영희 순서로 제비뽑기 진행 복원추출: 제비를 뽑으면 다시 주머니에 추가 비복원추출: 뽑힌 제비는 재사용하지 않음, 제거 복원 추출 철수의 확률 $\Longrightarrow$ 영희가 당청될 확률 철수의 당첨 사건 $\frac{2}{10}$ $\Longrightarrow$ $\frac{2}{10}$ 철수의 비당첨 사건 $\frac{8 ......

'파이썬 라이브러리를 활용한 머신러닝' 2장. 지도학습
2장. 지도학습 지도학습 “Input/Label”로 구성된 사례 데이터를 이용하여 ML 모델을 학습 최종 목표: 새로운 데이터를 정확하게 에측하는 것 유형: 회귀 & 분류 2.1 분류와 회귀 그림 1: 지도학습 요약 2.2 일반화, 과대적합, 과소적합 Generalization: 일반화 새로운 데이터에 정확한 예측을 제공하는 모델의 역량 모델이 복잡해 지면 학습셋에만 정확한 예측 제공 학습데이터에만 ......
![[til]기초 확률&통계#7: 확률 개념](https://taewanmerepo.github.io/2018/08/til20180802/list3.jpg)
[til]기초 확률&통계#7: 확률 개념
01. 확률의 개념 용어정리 Trial: 시행이란 동일한 조건에서 여러번 반복할 수 있고 그 결과가 우연에 의해서 결정되는 관찰이나 실험 예제: 주사위 던지기 Sample Space: 표본 공간 Trial(시행)의 결과들의 집합 예제 - 동전을 던지는 실험에서 표본 공간은 {앞면, 뒷면} - 6면 주사위를 던지는 실험에서 표본 공간은 {1, 2, 3, 4, 5, 6} Event: 사건 표본 공간의 부분 집합 fundamental e ......
![[til]기초 확률&통계#6: 이항정리](https://taewanmerepo.github.io/2018/08/til20180802/list2.jpg)
[til]기초 확률&통계#6: 이항정리
01. 이항정리 이항정리는?
$(a+b)^n$이 전개되는 방식을 정리 항이 두 개인 거듭제곱의 전개 방식을 소개 $(a+b)(a+b)=a^2+ab+ba+b^2$
$(a+b)(a+b)(a+b)$ : 8개의 항이 존재함 (2X2X2)
aaa aab aba baa abb bab bba bbb $a^3+3a^2+3ab^2+b^3$ = $a^3$: $_3C_0$=> 3개 중에서 b를 한개도 뽑지 않는 경우의 수 = $3a^2b$: $_3C ......
![[til]기초 확률&통계#5: 자연수 분할&집합분할](https://taewanmerepo.github.io/2018/08/til20180802/list.jpg)
[til]기초 확률&통계#5: 자연수 분할&집합분할
01. 자연수 분할 생각해 볼 거리1
5를 2개의 자연수 합으로 표현하는 방법 {1, 4}, {2, 3}, {3, 2}, {1, 4} : 순서를 고려할 필요 없음 2개 5를 3개의 자연수 합으로 표현 {3, 1, 1}, {2, 2, 1} n = n_1+n_2+n_3+……+n_k
n을 k개의 수로 분할할 수 있음 n>=n_1>=n_2>=n_3>=…..>=n_k 1 &l ......
1/2
»