01. 이항정리

• 이항정리는?

  • $(a+b)^n$이 전개되는 방식을 정리
  • 항이 두 개인 거듭제곱의 전개 방식을 소개

• $(a+b)(a+b)=a^2+ab+ba+b^2$

• $(a+b)(a+b)(a+b)$ : 8개의 항이 존재함 (2X2X2)

  • aaa
  • aab
  • aba
  • baa
  • abb
  • bab
  • bba
  • bbb
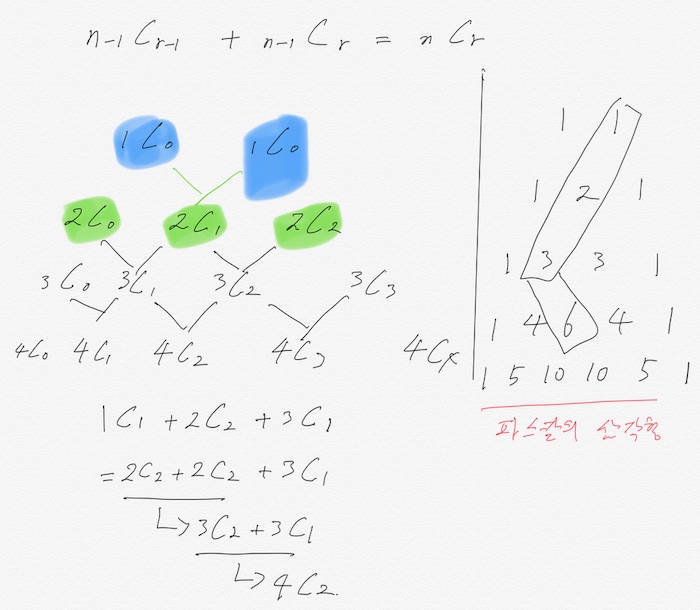
  • $a^3+3a^2+3ab^2+b^3$ = $a^3$: $_3C_0$=> 3개 중에서 b를 한개도 뽑지 않는 경우의 수 = $3a^2b$: $_3C_1$=> 3개 중에서 b를 한 개 뽑을 경우의 수 = $3ab^2$: $_3C_2$=> 3개 중에서 b를 두 개 뽑을 경우의 수 = #b^3$: $_3C_3$=> 3개 중에서 b를 세 개 뽑을 경우의 수

• $(a+b)(a+b)(a+b)(a+b)$ : 8개의 항이 존재함 (2X2X2)

  • $a^4$: $_4C_0$ => 4개 중에서 b를 한 개도 뽑지 않는 경우의 수 (1)
  • $a^3b$: $_4C_1$ => 4개 중에서 b를 한 개 뽑을 경우의 수 (4)
  • $a^2b^2$: $_4C_2$ => 4개 중에서 b를 두 개 뽑을 경우의 수 (6)
    
  • $a^1b^3$: $_4C_3$ => 4개 중에서 b를 세 개 뽑을 경우의 수 (4)
  • $b^4$: $_4C_4$ => 4개 중에서 b를 네 개 뽑을 경우의 수 (1)

$$ (a+b)^n = \sum_{r=0}^{4}{_rC_ra^{4-r}b^r} $$

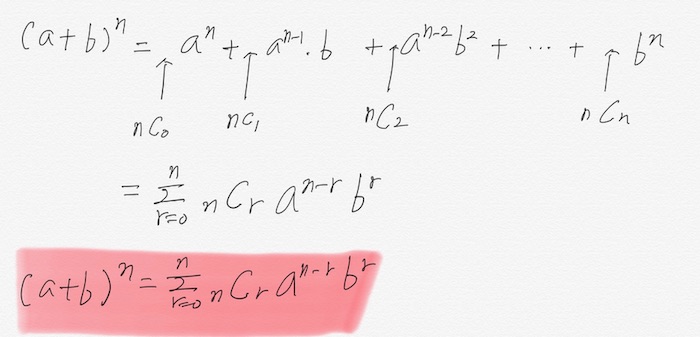
02. 이항계수의 성질 - Part 1

이항계수 성질 #1

$$ (1+x)^n = _nC_0x^0 + _nC_1x^1 + _nC_2x^2 + …. + _nC_nx^n $$

• 조건: x = 1
• 참고: $_nC_0$ = 1

$$ \begin{align} 2^n &= _nC_0x^0 + _nC_1x^1 + _nC_2x^2 + …. + _nC_nx^n \\
2^n - 1 &= _nC_1x^1 + _nC_2x^2 + …. + _nC_nx^n
\end{align} $$

이항계수 성질 #2

$$ (1+x)^n = _nC_0x^0 + _nC_1x^1 + _nC_2x^2 + …. + _nC_nx^n $$

• 조건: x = -1

$$ 0 = _nC_0 - _nC_1 + _nC_2 + - _nC_3 + …. + _nC_nx^n $$ $$ _nC_1 + _nC_3 + _nC_5 …. = _nC_0 + _nC_2 + _nC_4 …. $$ $$ T = _nC_1 + _nC_3 + _nC_5 …. = _nC_0 + _nC_2 + _nC_4 …. \\
2^n = T + T = 2T \\
T = 2^{n-1} $$

이항계수 성질 #3

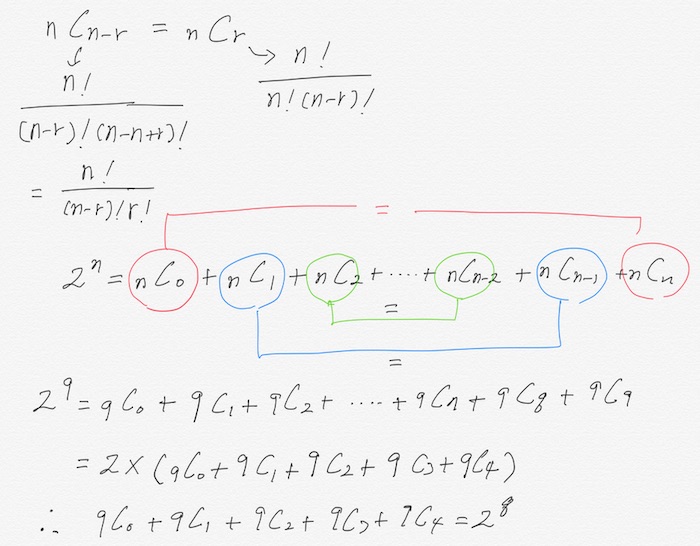
03. 이항계수의 성질 - Part 2

• 파스칼 삼각형