[til]기초 확률&통계#8: 확률 변수, 확률 분포, 이산확률 분포
01. 확률 변수, 확률 분포
확률변수, 확률 분포는 함수다.
- Sample Space는 시행에서 얻어지는 모든 결과의 집합.
- Sample Space의 모든 원소를 실수로 대응하는 함수: 확률 변수
- 확률 변수로 얻어진 실수를 확률값으로 변화하는 함수: 확률 분포
- 확률 변수와 확률 분포를 이용하여 시행의 결과를 실수로 변환할 수 있고, 발생 확률로 변환할 수 있다.
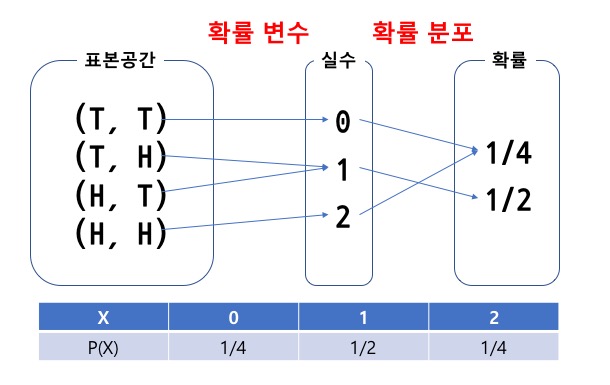
그림 1: 확률 변수와 확률 분포는 함수다
- 최종 확률분포표로 제시
02. 이산 확률 분포
- 확률 분포의 유형
- 연속 확률 분포: 확률 분포가 연속적인 것: 무수히 많은 것
- 정규분포
- 이산 확률 분포: 확률 분포가 불연속 적인 것
- 이항분포
- 연속 확률 분포: 확률 분포가 연속적인 것: 무수히 많은 것
이산 확률 분포
- 확률 분포가 셀수 있고 나열할 수 있는 분포
- 확률 분포는 실수를 확률로 변환하는 함수이다.
- 이산 확률 분포에서 확률 함수를 확률 질량 함수라고 한다.
이산 확률 분포의 특징
|X|x_1|x_2|x_3|….|x_n| |—-|—-|—-|—-|—-| |P(X)|p_1|p_2|p_3|….|p_n|
- $0 \leq P(X=x_i) \leq 1$
- 확률 분포에 나오는 확률값이 범위
- $\sum^{n}_{i=1}P(X=xi) = \sum^{n}{i=1}p_i= 1$
- $P(x_i \leq X \leq xj) = \sum^{j}{k=i}p_k$
3. 이산확률 변수의 기댓값
| X | 30 | 40 | 50 |
|---|---|---|---|
| 도수 | 2 | 3 | 1 |
| 확률 | 1⁄3 | 1⁄2 | 1⁄6 |
| 30*1⁄3 | 40*1⁄2 | 50*1⁄6 |
가능성(확률)로 계산한 평균: 기대값 $$ E(X)=\sum(x_i*P(x_i)) $$
평균과 기댓값의 차이
- 평균은 전체의 값에 대한 중간 값
- 기댓값은 전체가 아닌 확률로 계산한 평균
4. 이산환률 변수의 분산과 표준편차
- 평균은 값의 분포를 설명하지 못함
- 값이 떨어진 정도를 제공하는 개념 필요: 편차
- 편차: $Deviation = x_i - m$
- m: mean
- $V(X)=\frac{\sum^{n}_{i=1} Deviation^2}{n}$
- Variance
- 편차 제곱의 평균
- 분산이 크면 값은 떨어져 있음
- 기댓값과 분산
- $E(X) = meam$
- $V(X) = E[(X-m)^2]$
- 표준편차: Standard Deviation
- $\sqrt{V(X)} = \sigma(X)$
- $V(X) = E[(X-m)^2]=\sum(x_i-m)^2p_i$
- 표준편차가 크면 값들이 평균으로 부터 많이 떨어져 있음을 의미
$$ \begin{align} V(X) &= E[(X-m)^2]=\sum(x_i-m)^2p_i \\
&= \sum(x^2_ip_i-2mx_ip_i+m^2p_i) \\
&= \sum(x^{2}_ip_i)-2m\sum(x_ip_i)+m^2\sum p_i \\
&= E(X^2)-2mE(X)+m^2 \\
&= E(X^2)-2mm+m^2 \\
&= E(X^2)-m^2 \end{align} $$
5. 평균과 분산의 성질
이산환률 변수의 평균과 표준 편차의 성질
| x_1 | x_2 | x_3 | E(X) | etc | |
|---|---|---|---|---|---|
| X | 30 | 40 | 50 | 40 | E(X) |
| 2X | 60 | 80 | 100 | 80 | 2E(X) |
| X+30 | 60 | 70 | 80 | 70 | E(X)+30 |
- E(aX+b) (a, b는 실수, X는 확률 변수)
$$ \begin{align} E(aX+b) &= \sum_{i=1}^n(ax_i+b)p_i \\
&= \sum(ax_ip_i+bp_i) \\
&= \sum(ax_i p_i)+b \sum p_i \\
&= aE(X)+b*1 \\
&= aE(X)+b \end{align} $$
분산의 성질
| x_1 | x_2 | x_3 | E(X) | 편차 | etc | 편차^2 | |
|---|---|---|---|---|---|---|---|
| X | 30 | 40 | 50 | 40 | (-10, 0, 10) | 편차^2 | |
| 2X | 60 | 80 | 100 | 80 | (-20, 0, 20) | 편차도 2배 | 2X2 배 |
| X+30 | 60 | 70 | 800 | 70 | (-10, 00, 10) | 편차에 변화 없음 |
- $V(aX+b) = a^2V(X)$
- $\sigma(aX+b) = \sqrt{a^2V(X)} = a\sqrt{V(X)}=a\sigma(x)$
성질 요약
- E(aX+b) = aE(X)+b
- V(aX+b) = $a^2$V(X)
- $\sigma(aX+b) = |a|\sigma(X)$
