[til]기초 확률&통계#7: 확률 개념
01. 확률의 개념
용어정리
- Trial: 시행이란 동일한 조건에서 여러번 반복할 수 있고 그 결과가 우연에 의해서 결정되는 관찰이나 실험
- 예제: 주사위 던지기
- Sample Space: 표본 공간
- Trial(시행)의 결과들의 집합
- 예제 - 동전을 던지는 실험에서 표본 공간은 {앞면, 뒷면} - 6면 주사위를 던지는 실험에서 표본 공간은 {1, 2, 3, 4, 5, 6}
- Event: 사건
- 표본 공간의 부분 집합
- fundamental event: 근원 사건
- 원소의 갯수가 한 개인 사건
- 표본 공간이 한 원소로 이루어 집합
- 합사건: 두 사건 A와 B의 합집합으로 표현할 수 있는 사건
- $A \cup B$
- 예제: 4의 약수가 나오거나 또는 홀수가 나오는 사건 {1,2, 3, 4}
- 곱사건: 두 사건 A와 B의 교집합으로 표현할 수 있는 사건
- $A \cap B$
- 예제: 4의 약수 그리고 혹수 => {1}
- 여사건: 여집합으로 표현되는 사건
- $A^c$
- 예제: 4의 약수가 나오지 않는 사건
- 배반사건: A와 B 사전의 교집합니 공집합인 사건
- $A \cap B= \emptyset$
수학적 확률
- 수학적 확률은 근원 사건이 일어날 가능성이 모두 같을 때, 수학적 확률을 계산할 수 있다.
- 주사위에서 각 사간이 발생할 가능성은 모두 같음
- P(A): A라는 사건이 발생할 확률
$$
P(A) = \frac{n(A)}{n(S)}
$$
- S: 표본 공간
- 표본 공간의 원소의 객수로 사건의 원소의 객수를 나눈 것
- 확률이란 표본 공간의 원소이 객수 분에 사건의 원소의 갯수
- 수학적 확률은 표본공간과 사건이 모두 집합으로 정의된다.
- 집합에서 부분집합은 공집합과 전체 집합이 모두 부분 집합이다.
- n(A)=$\emptyset$ 일때
- P(A)=0, 공사건
- n(A)=S
- P(A)=1, 전사건
- 확률의 성질
- 0 <= P(A) <= 1
수학적 확률을 구하기 위해서는 경우의 수를 세거나 원소의 수를 셀 수 있어야 한다.
생각해 볼 거리
- 경우의 수와 요소의 수를 셀수 없다면 확률을 구할 수 없나?
기하학적 확률
- 양궁선수가 10점을 맞출 확률 (조건: 무조건 과녁안에는 맞춘다.)
- 면적의 분포로 계산
- 10점 영역 면적 / 전체 면적
통계적 확률
- 수학적 확률의 전제 조건은 근원사건이 일어날 확률이 모두 동일한 경우에 적용
- 통계적 확률은 근원 사건의 발생 확률이 다를 때 사용
- 경험적 확률:
- 예: 윳놀이 - 발생 확률이 1:1 아니다. 모양이 앞뒤가 다름 - 실제로 던져 본다. - $\frac{r}{n}$ - n은 총 횟수 - r은 위로 나온 경우의 수
- $\lim_{n\to\infty}\frac{r}{n}$ 로 모수를 처리 함
2. 수학적 확률
- 문제 1: 아래 그램과 같이 가운데를 제외하고 4개의 부분으로 나뉘어진 영역에 임의로 빨간색, 파란색, 노란색을 칠할 때 경계가 닿아 있는 역역끼리는 서로 아른 색으로 칠해질 확률은?
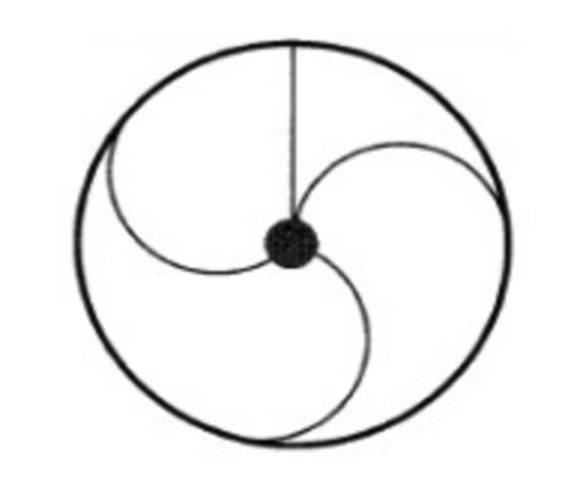
풀이
- 4개의 역역을 임의로 칠함
- $_3\Pi_4=3^4$
두 색이 연속으로 나오지 않을 경우의 수
- 4개 영역에 숫자를 표시
- 영역 1: 3
- 영역 2: 2
영역 3 - case 1: if 1번과 같은 색: ==> 영역4: 2 - case 2: if 1번과 다른 색: ==> 영역4: 1
3X2(2+1)=18
확률: 18⁄91 = 2⁄9
- 4개의 역역을 임의로 칠함
3. 확률 덧셈 정리 & 여사건 확률
확률의 덧셈 정리
- 집합의 원소 갯수
- n(A $\cup$ B) = n(A) + n(B) - n(A $\cap$ B)
$$ \begin{align} \frac{n(A \cup B)}{n(S)} &= \frac{n(A)}{n(S)} + \frac{n(B)}{n(S)} - \frac{n(A \cap$ B)}{n(S)} \\
P(A \cup B) &= P(A) + P(B) - P(A \cap B) \end{align} $$
- 문제: 1~20의 숫자 카드 중에서 2의 배수 또는 3의 배수일 확률
- $P(A \cup B) = P(A) + P(B) - P(A \cap B)$
- 사건 A: 2의 배수 = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
- 사건 B: 3의 배수 = {3, 6, 9, 12, 15, 18}
- 사건 A $\cap$ B = {6, 12, 18}
- 10⁄20 + 6⁄20 - 3⁄20 = 13⁄20
여사건의 확률
- A를 제외한 나머지 사건
- n(A)+n($A^c)=n(S)
- n(A) = n(S)-n($A^c)
$$ \begin{align} \frac{n(A)}{n(S)} &= \frac{n(S)}{n(S)} - \frac{n(A^c)}{n(S)} \\
P(A) &= 1 - P(A^c) \end{align} $$
- 문제: 남자가 3명, 여자가 2명인 집단에서 적어도 남자 1명이상 포함되는 확률?
- 여자가 대표가 되는 확률의 여사건의 확률
- p($A^c$) = 1 - $\frac{_2C_2}{_5C_2}$ = 1 - 1⁄10=0.9
04. 조건부 확률
- P(A|B)
- 사건 B가 발생했을 때, 사건 A가 발생할 확률
$$ P(A|B) = \frac{P(A \cap B)}{P(B)} $$
- 문제1: 카드 1-20에서
- 사건 A: 2의 배수가 나오는 사건
- 사건 B: 3의 배수가 나오는 사건
- 문제: 2의 배수가 나왔을때 3의 배수일 확률은?
$$
\begin{align}
P(B|A) &= \frac{P(B \cap A)}{P(A)} \\
&= \frac{\frac{3}{20}}{\frac{1}{20}} \\
&= 0.3
\end{align}
$$
- 조건부 확률의 의미
- 표본 공간이 주어진 사건의 상황으로 바뀌는 확률
- 주어진 사건의 상황으로 표본 공간이 변화
- 문제2: 한명을 뽑았을 때, 남학생이 안경을 쓸 확률은?
| 안경 | 안경X | |
|---|---|---|
| 남학생 | 5 | 7 |
| 여학생 | 6 | 4 |
- 풀이
- 사건A: 남학생일 사건
- 사건B: 안경을 쓸 사건
- $p(B|A)=\frac{P(A \cap B)}{p(A)}$
$$
\begin{align}
p(B|A) &= \frac{P(A \cap B)}{p(A)} \\
&= \frac{\frac{5}{22}}{\frac{12}{22}} = \frac{5}{12}
\end{align}
$$
- 표본공간이 사건 A로 변경됨
05. 확률의 곱셈 정리
$$
\begin{align}
P(A)P(B|A) &= {P(A)}\frac{P(A \cap B)}{P(A)} \\
&= P(A \cap B)
\end{align}
$$
- 문제 1: 10장의 제비뽑기가 있다. 당청 제비는 2장이다. 철수와 영희가 순서대로 제비를 뽑을 때, 모두 당첨될 확률?
- 비 복원 추출
- 풀이
- 사건A: 철수가 당첨될 확률
- 사건B: 영희가 당첨될 확률
- 철수와 영희가 당청될 확률
$$ \begin{align} P(A \cap B) &= P(A)P(B|A) \\
&= \frac{2}{10} * \frac{\frac{2}{10} \frac{1}{9}}{\frac{2}{10}} \\
&= \frac{2}{10} * \frac{1}{9} \\
&= \frac{1}{45} \end{align} $$ - p(A $\cap$ B)의 의미: A사건이 발생할 확률과 A사건이 발생할 조건에서 사건 B가 발생할 확률의 곱
P(B|A)는 다음과 같이 읽습니다. “P B given A”
