01. 자연수 분할

• 생각해 볼 거리1

  • 5를 2개의 자연수 합으로 표현하는 방법
    • {1, 4}, {2, 3}, {3, 2}, {1, 4} : 순서를 고려할 필요 없음
    • 2개
  • 5를 3개의 자연수 합으로 표현
    • {3, 1, 1}, {2, 2, 1}

• n = n_1+n_2+n_3+……+n_k

  • n을 k개의 수로 분할할 수 있음
  • n>=n_1>=n_2>=n_3>=…..>=n_k
  • 1 <= k <= n
  • example
    • 5
    • k=1 ==> {5}
    • k=5 ==> {1,1,1,1,1}

• 자연수 n을 n보다 작거나 같은 k개의 자연수의 합으로 순서를 고려하지 않고 표현한 것은 자연수의 분할 이라고 한다.

• 분할에 대한 표기법

• P(n, k) = 자연수 n을 k개의 자연수의 합으로 표현의 경우의 수

  • Partition
  • Partition n k
  • example
    • p(5, 2) = {3, 2}

• 자연수 n의 불할의 수

  • 자연수 n을 n개 이하의 자연수로 표현할 수 있는 총 가지 수
    • p(n, 1)+p(n, 2)+p(n, 3)+….+p(n, n-1)+p(n, n)
  • example: 5의 분할의 수
    • p(5, 1) = 1, {5}
    • p(5, 2) = 2, {4, 1}, {3, 2}
    • p(5, 3) = 2, {3, 1, 1}, {2, 2, 1}
    • p(5, 4) = 1, {2, 1, 1, 1}
    • p(5, 5) = 1, {1, 1, 1, 1, 1}
    • total: 7

p(n, k)의 성질

• 성질 1

  • p(n, 1) = 1
  • p(n, n) = 1
  • p(n, k) = 0 if k>n

• 성질 2

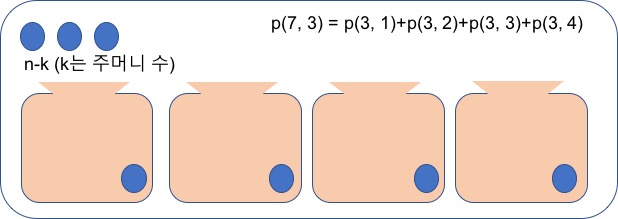
  • p(n, k) = p(n-k, 1) + p(n-k, 2) + …. +p(n-k, k)
  • exmaple
    • p(7, 4) = 자연수 7을 자연수 4개로 나타내는 방법
      • 4개의 주머니에 공 7개를 분할아여 채우며, 모든 주머니는 1개 이상의 공을 갖고 있어야 함

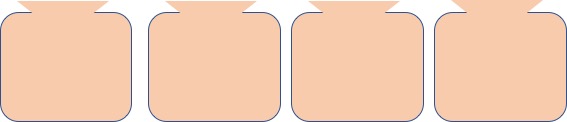
• 각 주머니에는 1개의 공이 있어야 함
  • 나머지 3개의 공을 4개의 주머니에 담는 경우의 수와 같음

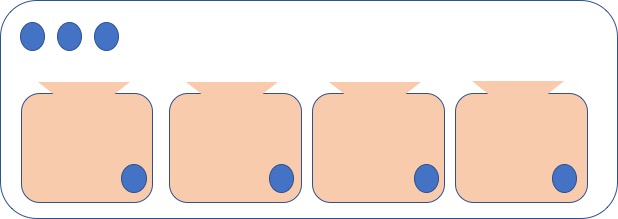
• 성질 3
  • p(n,k) = p(n-1, k-1)+ p(n-k, k)
  • example
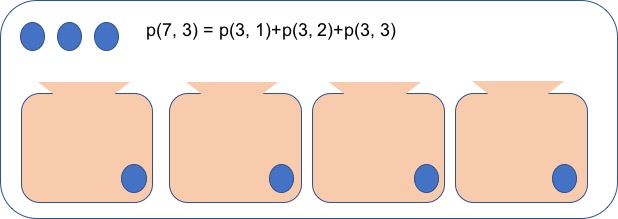
    • p(7,3) = 7을 3개의 자연수의 합을 표현하는 경우의 수
    • 1을 포함하는 것과 1을 포함하지 않는 경우로 구분
      • 1+a+b => p(6, 2)
      • a+b+c (a, b, c는 모두 2 이상의 자연수) ==> p(4, 3)
        • a=A+1, b=B+1, c=C+1
        • A+B+C+3 = 7
        • A+B+C=4
        • P(4, 3)
          

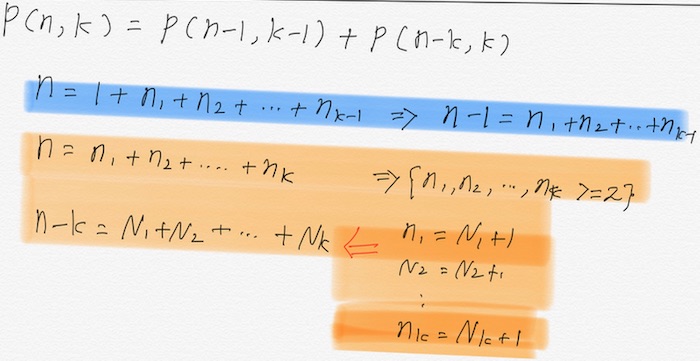
• 성질 3의 예제
  • p(7, 4) = p(6, 3) + p(3, 4)
  • p(7, 4) = p(6, 3) + 0
  • p(3, 4) = 경우의 수 0, 자연수 3을 4개의 자연수 합으로 표현할 수 없음

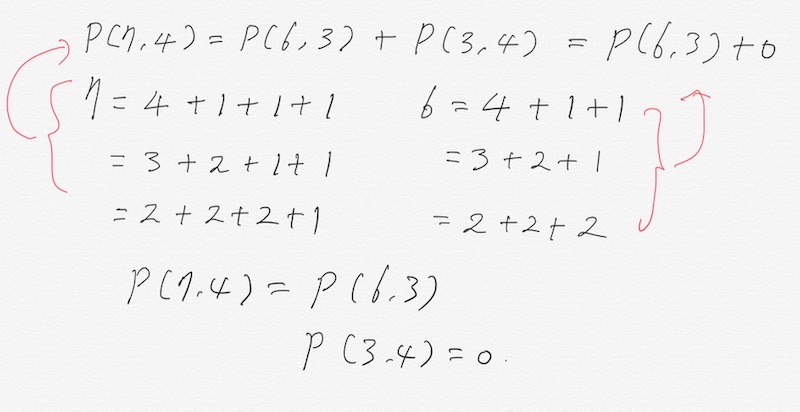
2. 집합의 분할

• {a, b, c} 집합을 부분집합이 합집합으로 표현할 수 있다.
• { a, b, c }
  • {a} $\cup$ {b, c}
  • {b} $\cup$ {a, c}
  • {c} $\cup$ {a, b}

• 특징

  • 두 부분 집합은 전체이 부분집합
  • 두 부분 집합은 공집합은 아니다
  • 교집합이 공집합인 서로소

• 집합의 분할

  • 원소가 유한개인 집합을 공집합이 아니면서 서로소인 집합인 몇 개의 부분 집합의 합집합으로 나타내는 것

• A = {a, b, c, d}, s(4, 2)

  • 원소가 4개인 집합을 2개의 서로소인 부분 집합의 합집합으로 표현하는 경우의 수
  • 원소의 객수를 (1, 3)으로 분할하는 것과 (2, 2) 분할
  • (1, 3)
    • {1}, {2, 3, 4}
    • {2}, {1, 3, 4}
    • {3}, {1, 2, 4}
    • $_4C_1 * _3C_3=4$
  • (2, 2)
    • $_4C_2 * _2C_2 / 2!=3$
  • 4+3 ==> 7 가지

• 원소의 갯수가 n 개인 집합 A의 분할의 수

  • s(n, 1)+s(n, 2)+…+s(n, n)

• s(n, k)의 성질

  1. s(n, 1) = 1
     • {a, b, c}={a, b, c}
  2. s(n, n) = 1
     • {a, b, c}= {a} $\cup$ {b} $\cup$ {c}
  3. 1<k<n, S(n, k) = S(n-1, k-1)+k*S(n-1, k)
     
     • {a, b, c, d}의 S(4, 3)
       • 4개의 원소 집합을 3개 부분집합의 합집합으로 하는 경우의 수?
       • {a}를 포함하는 집합: S(3, 2)
       • {a}를 단독으로 포함하지 않는 집합
         • {b}$\cup$ {c}$\cup$ {d}
         • {a}를 포함하는 경우의 수: 3배
           • {ab}$\cup$ {c}$\cup$ {d}
           • {b}$\cup$ {ac}$\cup$ {d}
           • {b}$\cup$ {c}$\cup$ {ad}
             
     • S(4, 3)=S(3, 2)+3S(3, 3)

• {1, 2, 3, 4} 집합의 모든 분할 경우의 수?