[til]기초 확률&통계#4: 조합
1. 조합
- 순열(Permutation): 순서있게 나열하는 방법의 수
- $_nP_r$: n개중에서 r개를 뽑아서 순서 있게 나열한 수
- $\frac{n!}{(n-r)!}$
- 조합(Combination): 순서를 고려하지 않고 선택하는 방법의 수
- 순열을 순서를 고려한 경우의 수임
- 조합은 순서를 고려하지 않음
- 순열의 객수에 선택한 갯수의 경우의 수로 나워서 순열의 중복을 제거
- 순열의 순서를 제거 => $_nC_r = \frac{_nP_r}{r!}$
- 예제
- ABCDE 중에서 2개를 뽑아서 순서있게 나열하는 것
- $_5P_2$
- ABCDE 중에서 2개를 조합
- 순서를 고려하지 않음
- 선택만 함
- 5개 중에서 2개를 선택하는 것
- $_5C_2$ = $\frac{_5P_2}{2!}$
- ABCDE 중에서 2개를 뽑아서 순서있게 나열하는 것
$$_nC_r=\frac{_nP_r}{r!}=\frac{n!}{(n-r)!r!} $$ - n개중 r개를 순서를 고려하지 않고 선택하는 방법의 수
조합의 이해
- 1반은 10명이다. 10명 중에서 회장과 반장 2명을 선출하는 경우의 수
- 2명을 선정함에 있어서 순서의 구분이 있음
- 순서가 중요함
- 순열
- $_10P_2=\frac{10!}{8!}=90$
- 1반의 대표를 2명 뽑는다. 반은 전체가 10명이다.
- 순서가 중요하지 않음
- Combination
- $_10C_2=\frac{10!}{8!2!}=45$
조합의 성질
$$_nC_r=\frac{_nP_r}{r!}=\frac{n!}{(n-r)!r!} $$
- 5개 중에서 순서 없이 2개를 선택하는 방법의 수와 5개 중에서 순서 없이 3개를 선택하는 방법의 수 비교
$$\begin{align} _5C_2 &= \frac{5!}{3!2!} \\
_5C_3 &= \frac{5!}{2!3!} \\
_5C_2 &= _5C_3 \end{align}$$
- Combination 성질1
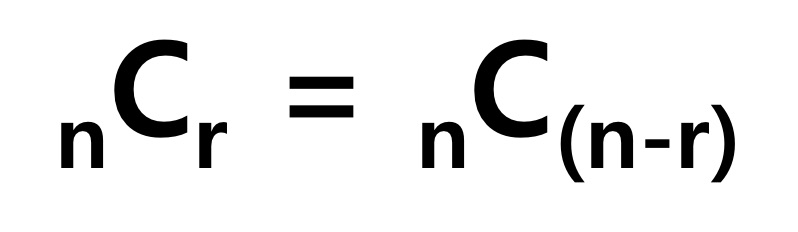
- Combination 성질2
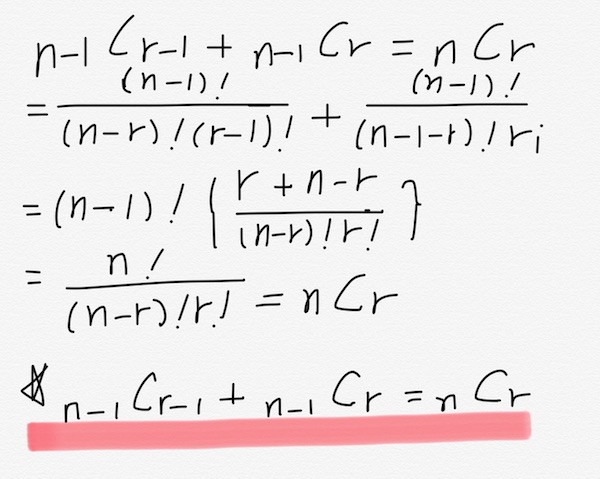
- n-1개 중에서 r-1개를 순서없이 선택하는 방법의 수와 n-1개 중에서 r개 선택하는 방법의 수는 n개 중에서 r개 순서 없이 선택하는 방법의 수와 같다.
2. 중복 조합
- 중복조합: 중복된 선택이 가능한 순서를 고려하지 않은 경우의 수
- 중복 허용
- 순서 고려 하지 않음
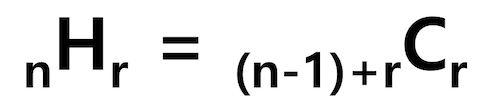

- 문제 1
- 중국집 주문 메뉴
- 중국집에 5명 손님 입장
- 주문 가능한 메뉴: 짜장면, 짬뽕, 볶음밥
- 주방장 입장의 경우의 수
- 풀이
- 중복을 허용한다
- 순서를 고려할 필요가 없음
- $_3H_5=_7C_5=\frac{7!}{5!2!}=21$
- 중국집 주문 메뉴
- 문제 2
- $x+y+z=7$
- x, y, z는 음이 아닌 정수
- x, y, y의 해의 수는?
- 풀이
- $_3H_7=_9C_7=\frac{9!}{7!2!}=32$
3. 조 나누기
- A, B, C, D를 2개씩 두 그룹으로 나누고 싶다.
- $_4C_2$ 로 생각하기 쉽다.
- 조 나누기 입장에서 적용할 수 없음
- $_4C_2$는 1조의 경우의 수를 결정하는 것
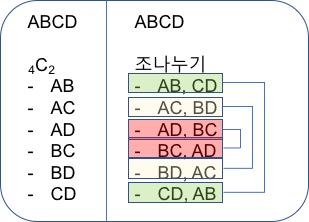
- 조 나누기의 경우 순서가 없는 조건이 2가지
- 조 구성원의 순서가 없음
- 조의 순서가 없음
$$\frac{_4C_2}{2!} = 3 $$
예제 3-1
- 6명을 3명씩 2개 조로 나누는 경우의 수는?
- 6명에서 3명을 뽑아서 1조를 만들면 나머지는 다른 조가 됨
- 조 구성원의 순서가 없음
- 조의 순서강 없음
- $\frac{_6C_3}{2!}=10%
- 6명을 3명씩 2개 조로 나누는 경우의 수는?
예제 3-2
- 2명의 첫번째 조를 만드는 경우의 수: 6C2 = 15
- 나머지 4명에서 2명의 조를 만드는 경우의 수: 4C2 = 6
- 두 경우의 수는 동시 조건: 15*6=90
- 조의 순서는 무의미: 3! 경우의 수로 나눔
- 15개
- 6C2 X 4C2 X 2C1 / 3!
예제 3-3
- 명수가 값은 조가 없기에 순서의 의미가 발생
- 6명을 1명, 2명, 3명으로 나누는 조나누기의 경우의 수
- 6C3 X 3C2 X 1C1 = 20 X 3 X1 = 60
- 조의 순서가 의미가 있음
예제 3-4
- 7명을 3, 3, 1명으로 나누는 경우의 수
- 2개의 조가 인원수가 같아서 순서의 의미가 2 조에개만 발생
- 7C3 X 4C3 / 2!=
# 1개로 간주
{ABC}{DEF}{G}
{DEF}{ABC}{G}
n!는 크기가 같은 그룹의 수 $$ \frac{_nC_r}{n!} $$
예제 3-5
- 8명을 2, 2, 2, 2로 조를 구분하는 방법
- $\frac{_8C_2 X _6C_2 X _4C_2 X _2C_2}{4!}$
- 8명을 2, 2, 2, 2로 조를 구분하는 방법
예제 3-6
- 4명을 2개 조로 구분하고 김감독과 이감독이 지도를 각각 맡을 경우의 수
- 2명씩 2개 조로 나눌 때, Combination / 그룹수로 중복을 제거
- 김감독과 이감독에게 분배할 경우 순서가 다시 발생 배분 그룹 수의 경우의 수의 곱
- $\frac{_4C_2 * _2C_2}{2!}*2!$
- 조나누기 후에 분배가 발생하면 기본 Combination으로 복원 됨
