1. 원순열

• 순열: 일렬로 순서있게 나열하는 방법, 처음과 끝이 존재
• 원순열: 처음과 끝이 없는 상태로 순서있게 나열하는 방법, 원위에 나열하는 개념
  • 처음과 끝이 없다
  • 한방향으로 요소의 나열 순서가 같으면 같은 것으로 간주

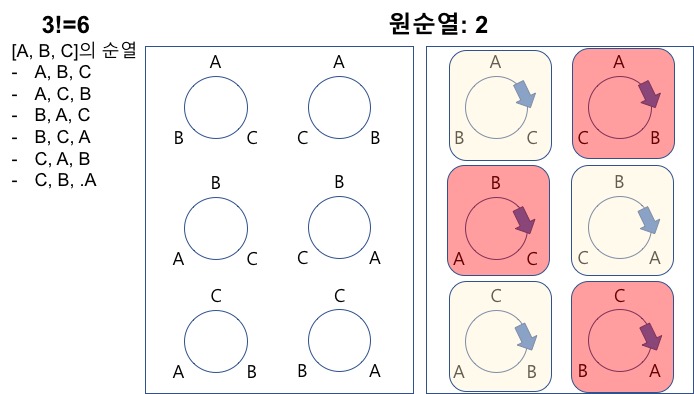
• 처음과 끝이 없는 순열에 처음과 끝을 만드는 방법
  • 첫번째 요소를 고정하여 기준으로 처음과 끝을 만듦
  • 첫번째 요소는 모든 요소가 위치할 수 있음
  • 전체 순열의 수에서 첫 번째 요소에 올 수 있는 요소 수를 나누면 원수열의 갯수가 됨
  • 첫번째 요소는 기준을 정하는 역할을 담당할 뿐 경우의 수에 미치는 영향이 없어짐

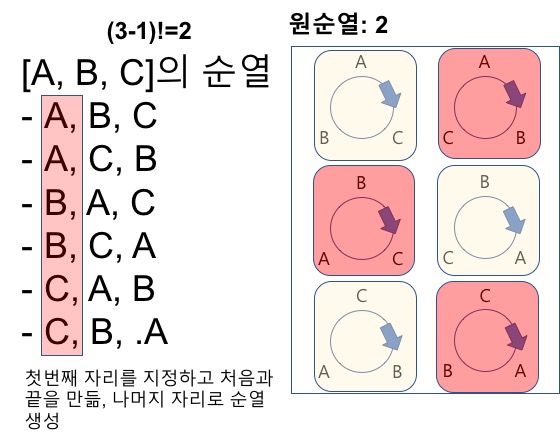
$$ 원순열= /frac{n!}{n} = (n-1)! $$

응용

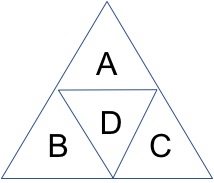
• 위 그림 4 영역을 서로 다른 색으로 칠하는 경우의 수

• 풀이
  • 가운데 영역과 주변 영역을 분리하여 생각
  • 주변 영역은 완벽한 대칭이기에 원순열로 간주
  • 사건1: 가운데에 칠할 수 있는 경우의 수: 4가지
  • 사건2: 주변은 가운데 책을 제외한 3개의 색을 칠하는 원수열
  • (3-1)!
  • 사건1과 사건2는 동시에 발생하는 사건
  • 곱의 법칙 적용
  • 4X2=8
• 생각해 볼 것
  • 원의 모양이 아니더라도 처음과 끝이 없고 대칭성의 모양은 원순열로 간주할 수 있음

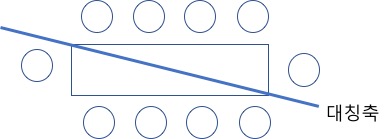
2. 원순열의 응용

• 일종의 다각형 순열
• 원순열처럼 보이지만 그룹이 나눠지는 순열

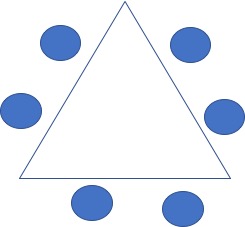
• 위 순열을 원순열로 비교해 보면 다음과 같은 경우에 원순열에서는 1개로 간주하지만 다각형 순열에서는 2개로 간주한다.

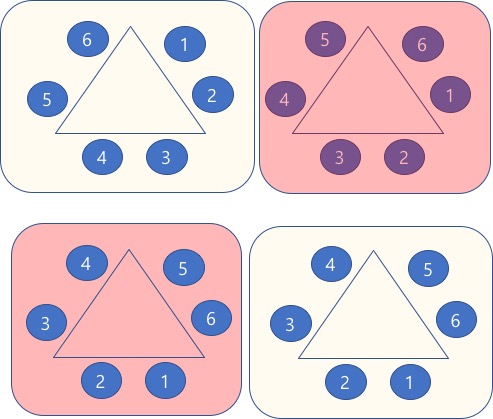
• 한면에서 그룹이 되는 쌍의 영향을 받음
• (6-1)!X2
• 원순열 개수 X 면의 요소수(그룹의 분할 갯수)
• 순열 / 면의 수 (그룹 개수)

응용

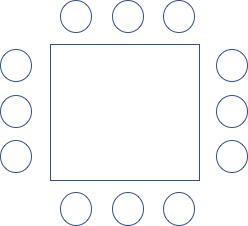
• 위 그림 순열의 개수는?
• (12-1)! X 3
  

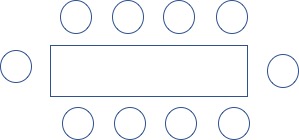
• 위 그림 순열의 개수는?
• (7)! X 4
• 대칭축을 기준으로 그룹의 갯수는 4