1. 경우의 수

• 합의 법칙: 동시에 일어나지 않는 사건 (각 사건의 경우의 수 합)
• 곡의 법칙: 동시에 일어나는 혹은 연달아 일어나는 두 사건(가 사건의 경우의 수 곱)

Case1 - 합의 법칙 사례

• 문제: 1-10 카드 10장 중에서 2장을 선택하여, 두 합이 7의 배수가 되는 경우의 수

• 풀이
  • 두 장의 카드 합의 크기 범위: $3<= A+B <= 19$
  • 가능한 7의 배수: {7, 14}
  • 두 카드를 선택할 때 순서는 중요하지 않음
  • 두 카드의 합 7: (1, 6) (2, 5) (3, 4)
  • 두 카드의 합 14: (4, 10) (5, 9) (6, 8)
  • 7이 되는 사건과 14가 되는 사건은 동시에 발생할 수 없음
  • 합의 법칙 적용
  • 경우의 수 = 두 카드의 합 7의 경우의 수 + 두 카드의 합 14의 경우의 수 = 6

Case2 - 합의 법칙 사례

• 문제: 자연수 x와 y가 있다. x와 y의 합이 4보다 같거나 작은 (x, y)의 순서쌍의 경우의 수는?

• 풀이
  • x+y의 범위: $2<= x+y <=4$
  • 사건별 경우의 수
  • x+y==2: (1, 1)
  • x+y==3: (1, 2), (2, 1)
  • x+y==4: (1, 3), (2, 2), (3, 1)
  • 각 사건은 동시에 발생할 수 없음
  • 합의 법칙 적용
  • 경우의 수: 1 + 2 + 3 = 6
  • 전체 경우의 수: 6개

Case3 - 곱의 법칙 사례

• 문제: 주사위 2개를 던질때 일어날 경우의 수

• 풀이
  • 첫번째 주사위 경우의 수: 6개
  • 두번째 주사위 경우의 수: 6개
  • 각 사건은 동시에 발생할 수 있음
  • 곱의 법칙 적용
  • 경우의 수: 6 X 6
  • 전체 경우의 수: 36개

Case4 - 곱의 법칙 사례

• 문제: 24의 양의 약수의 갯수

• 풀이
  • 약수는 소인수 분해 결과의 곱
  • $24=2^3X3$
  • 약수 = a X b
    • $a \in { 2^0, 2^1, 2^2, 2^3 }$
    • $b \in { 3^0, 3^1 }$
  • a의 사건 경우의 수: 4
  • b의 사건 경우의 수: 2
  • 두 사건은 동시발생: 4 X 2
  • 전체 경우의 수: 8

Case5 - 곱의 법칙 사례

• 문제: (a + b)(x + y + z) 항의 갯수

• 풀이
  • 두 사건은 동시발생: 2 X 3
  • 전체 경우의 수: 6

Case6 - 합의 법칙과 곱의 법칙

• 문제: 다음 그림과 같은 A, B, C, D의 경로가 있을 때, A에서 D로 가는 경로의 경우의 수

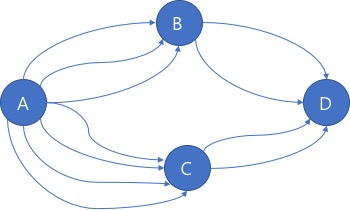
• 풀이
  • 동시 발생 사건:
    • Case 1: A-B-D
    • Case 2: A-C-D
  • 독립 발생 사건: Case 1, Case2
    
  • Case1: 4X2
  • Case2: 3X2
  • 전체 경로: 8 + 6 = 14

2. 순열

• 순열(Permutation): 순서있는 나열

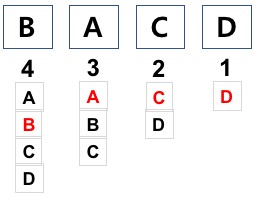
• A, B, C, D 일렬로 나열하는 경우의 수

  • 나열하는 경우의 수는 동시에 발생하는 사건
  • 4 X 3 X 2 X 1 = 4!
  • n! = n x (n-1) x …. x 2 x 1

• 문제: A, B, C, D, E 중에서 3개를 선택하여 나열하는 경우의 수

• 동시에 발생
• 5 X 4 X 3
• $_nP_r$
• $\frac{5!}{3!}$

Permutation

• n개 중에서 r개를 뽑아서 일렬로 나열하는 경우의 수

$$ \begin{align} _nP_r &= \frac{n!}{(n-r)!} \\
&= n X (n-1) X … (n-r+1) \end{align} $$

순열: 이웃하는 경우의 수

• 문제: ABCDE 5개 문자 중에서 A와 B가 연속될 경우의 수

• 솔루션

  • AB를 하나의 묶음으로 간주
  • {AB}CDE의 경우의 수를 계산
  • AB는 순서에 대한 구분이 있음
  • $_4P_4 *_2P_1$
  • 4 X 3 X 2 X 2 = 48

• 문제: ABCDE 5개 문자 중에서 ABC가 연속될 경우의 수

• 솔루션

  • {ABC}DE
  • 3! * 3!
  • 6 X 6 = 36

• 문제: ABCDEF 6개 문자 중에서 {AB} {CD} {EF} 일 경우의 수는?

• 솔루션

  • 3! * 2! * 2! * 2!
  • 6 X 2 X 2 X 2 = 48

순열: 이웃하지 않는 경우의 수

• 문제: ABCDE가 있다. AB가 이웃하지 않는 경우의 수를 계산 하시오.

• Solution 1
  • 방법
    • 이웃해도 되는 놈들을 먼저 나열: CDE
    • 사이사이 및 양쪽 끝에 이웃하면 안되는 것을 끼워 넣음 {1}C{2}D{3}E{4}
    • 두 사건은 동시에 발새아는 사런, 곱의 법칙 적용
  • 이웃해도 되는 것을의 나열: 3!=6
  • 사이사이 및 양쪽 끝에 이웃하면 안되는 것을 끼워 넣음: $_4P_2=/frac{4!}{2!}=12$
  • 곱의 법칙: 6*12=72

• Solution 2

  • 방법
    • 전체 5개의 순열을 계산
    • AB가 이웃하는 순열을 계산
    • 전체에서 AB가 이웃하는 순열을 제외
  • 전체 5개의 순열을 계산: 5!=120
  • AB가 이웃하는 순열을 계산: 4!*2=48
  • 전체에서 이웃한 경우의 수를 제외: 120-48=72

• 문제: ABCDEFG가 있다. AB가 반드시 이웃해야 하고 CD는 반드시 떨어져 있어야 하는 경우의 수

• Solution1
  • 이웃해도 되는 놈들을 먼저 나열: {AB}EFG = 4!X2 =48
  • 사이사이 및 양쪽 끝에 이웃하면 안되는 것을 끼워 넣음 [1]{AB}[2]E[3]E[4]G[5]: $_5P_2=/frac{5!}{3!}=20$
  • 두 사건은 동시에 발새아는 사런, 곱의 법칙 적용: 48X20=960
• Solution2
  • AB가 이웃할 전체 경우의 수 계산 = 6!X2 = 1440
  • AB가 이웃하고 CD가 이웃할 경우의 수 계산 {AB}{CD}EFG= = 5!X2X2 = 480
  • 전체에서 제외 = 960