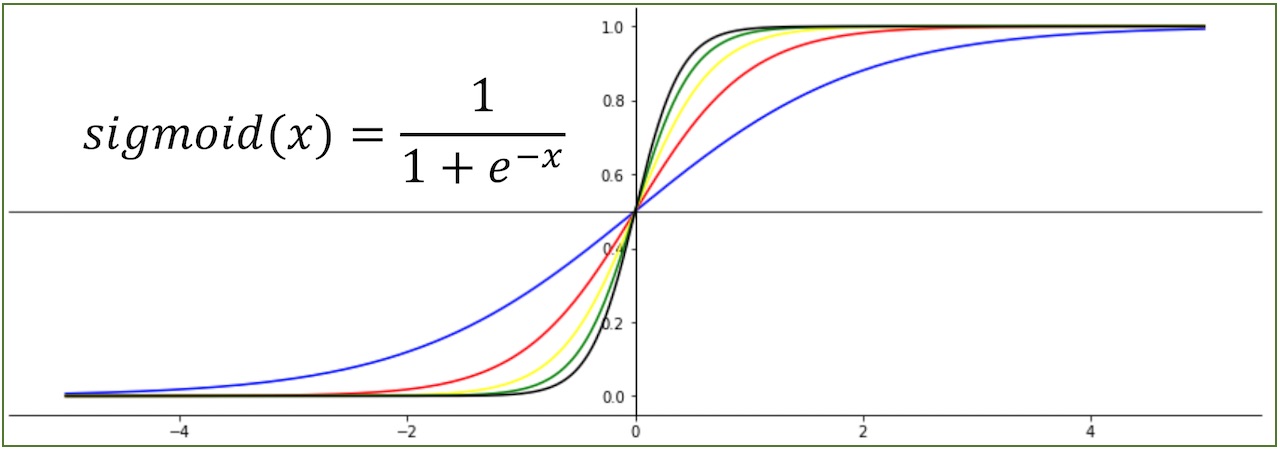
Sigmoid 함수는 S자와 유사한 완만한 시그모이드 커브 형태를 보이는 함수입니다. Sigmoid는 대표적인 Logistic 함수입니다. Sigmoid 함수는 모든 실수 입력 값을 0보다 크고 1보다 작은 미분 가능한 수로 변환하는 특징을 갖습니다. 모든 입력에 대하여 sigmoid는 S와 같은 형태로 미분 가능한 0~1 사이의 값을 반환하기에 Logistic Classification과 같은 분류 문제의 가설과 비용 함수(Cost Function)¹에 많이 사용됩니다. sigmoid의 반환 값은 확률형태이기 때문에 결과를 확률로 해석할 때 유용합니다.

딥러닝에서는 노드에 임계값을 넘을 때만 출력하는 활성 함수로도 이용됩니다. Sigmoid 함수는 마이너스 값을 0에 가깝게 표현하기 때문에 입력값이 최종 계층에서 미치는 영향이 적어지는 Vanishing gradient problem 이 발생합니다. 이 문제 때문에 현재 딥러닝 실무에서 사용되지는 않지만, 딥러닝 입문 과정에서 꼭 다루는 함수입니다.

Sigmoid 함수는 미분 결과가 간결하고 사용하기 쉬우므로 초기에 많이 사용되었습니다. 머신 러닝에서 Sigmoid함수는 가설과 학습에서 사용됩니다. 학습에 사용될 때는 Sigmoid를 미분한 결과가 사용됩니다. sigmoid는 미분 결과를 프로그래밍하기 쉽기에 인기가 더욱 높았습니다.

아래에서 Sigmoid 함수의 실체와 미분 유도 과정을 살펴보겠습니다.

Sigmoid 함수

Sigmoid 함수는 다음과 같이 정의 됩니다.

$$sigmoid(x) = \frac{1}{1+e^{-x}}$$

Sigmoid 함수 미분

Sigmoid를 Logistic Classification의 가설로 사용하거나 딥러닝의 활성함수로 사용할 경우 경사 하강법(Gradient Descent Algorithm) 계산 혹은 역전파 계산 과정에서 Sigmoid 함수의 미분이 사용됩니다. 이런 과정의 이해를 돕는 목적으로 sigmoid의 미분 과정을 정리합니다.

sigmoid 미분 과정

sigmoid 함수 미분 절차는 다음과 같습니다.

$$ \begin{align} \frac{d}{dx}sigmoid(x) & = \frac{d}{dx}{(1+e^{-x})^{-1}} \\
& = (-1)\frac{1}{(1+e^{-x})^{2}}\frac{d}{dx}(1+e^{-x}) \\
& = (-1)\frac{1}{(1+e^{-x})^{2}}(0+e^{-x})\frac{d}{dx}(-x) \\
& = (-1)\frac{1}{(1+e^{-x})^{2}}e^{-x}(-1) \\
& = \frac{e^{-x}}{(1+e^{-x})^{2}} \\
& = \frac{1+e^{-x}-1}{(1+e^{-x})^{2}} \\
& = \frac{(1+e^{-x})}{(1+e^{-x})^{2}}-\frac{1}{(1+e^{-x})^{2}} \\
& = \frac{1}{1+e^{-x}}-\frac{1}{(1+e^{-x})^{2}} \\
& = \frac{1}{1+e^{-x}}(1-\frac{1}{1+e^{-x}}) \\
& = sigmoid(x)(1-sigmoid(x)) \end{align} $$

sigmoid 미분 결과

sigmoid의 미분 결과(도함수)는 다음과 같습니다. 앞에서 언급한 것처럼 sigmoid의 미분 결과는 매우 간결한 것 을 확인할 수 있습니다.

$$ \frac{d}{dx}sigmoid(x) = sigmoid(x)(1-sigmoid(x)) $$

다음은 sigmoid 미분결과(도함수)로 그래프를 그린 결과입니다.

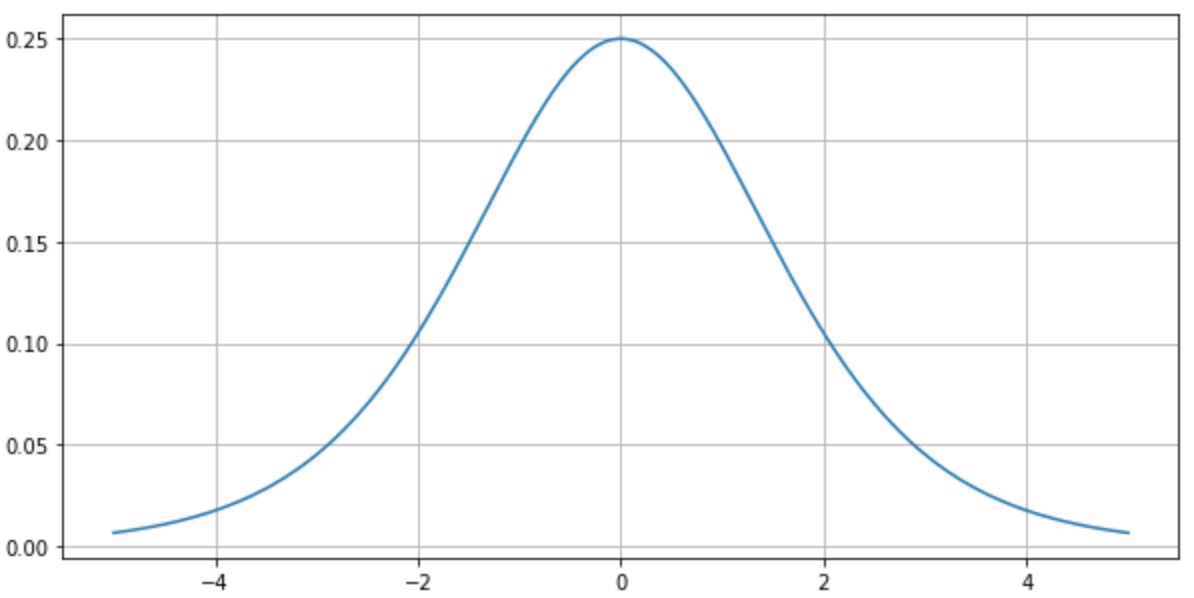
그래프의 미분계수를 보면 최댓값은 0.25입니다. deep learning에서 학습을 위하여 역전파(Backpropagation)를 계산하는 과정에서 activation function의 미분 값을 곱하는 과정이 포함됩니다. sigmoid를 활성 함수로 사용하는 경우 은닉층의 깊이가 깊다면 오차율 계산이 어렵다는 문제가 발생합니다. 이것이 딥러닝에 sigmoid를 사용할 때 “vanishing gradient problem“이 발행하는 이유입니다.

sigmoid 함수 구현

sigmoid 코드 구현은 매우 간단합니다. sigmoid의 구현 코드를 정리합니다.

파이썬 구현

파이썬으로 구현한 sigmoid 함수는 다음과 같습니다.

import math

def sigmoid(x, deff=False):
  if deff:
    return sigmoid(x)*(1-sigmoid(x))
  else:
    return 1 / (1 + math.exp(-x))

scala 구현

스칼라로 구현한 sigmoid 함수는 다음과 같습니다.

import scala.math

def sigmoid(x: Double): Double = {
  return 1.0 / (1.0 + math.pow(math.E, -x))
}

참고자료

• https://en.wikipedia.org/wiki/Sigmoid_function
• CHAPTER 5.Why are deep neural networks hard to train?