코사인 제 1법칙과 제 2법칙을 정리합니다.

코사인 제 1법칙

코사인 제 1법칙은 삼각형의 꼭지각의 코사인과 변 사이에는 일정한 관계를 식으로 나타낸 법칙입니다.

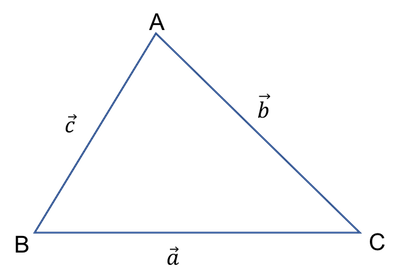
위와 같은 삼각형은 다음과 같은 코사인 제 1법칙이 적용됩니다.

$$ \begin{align} a & = ccosB + bcosC \\
b & = ccosA + acosC \\
c & = bcosA + acosB \end{align} $$

코사인 제 1법칙은 다음과 같은 의미를 갖습니다.

두 각을 알고 두 각의 빗변의 길이를 알면 밑변의 길이를 구할 수 있다.

코사인 제 1 법칙 증명: 예각 삼각형

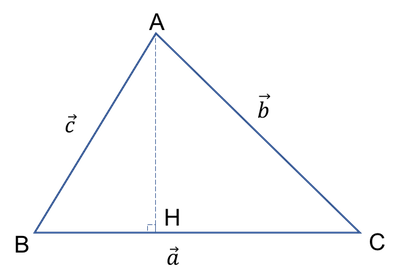
$$ \begin{align} \overline{a} &= \overline{BH} + \overline{HC} \end{align} $$

$\overline{BH}$와 $\overline{BC}$의 길이는 cos을 이용하여 다음과 같이 구할 수 있습니다.

$$ \begin{align} \overline{BH} &= \overline{c} * cosB \\
\overline{HC} &= \overline{b} * cosC \end{align} $$

두 변의 길이를 이용하여 다음과 같은 식을 만들 수 있습니다.

$$ \begin{align} \overline{a} &= \overline{BH} + \overline{HC} \\
&= \overline{c}cosB + \overline{b}cosC \end{align} $$

코사인 제 1법칙 증명: 직각 삼각형

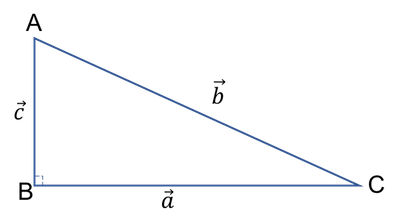
직각 삼각형은 다음과 같이 코사인 제 1법칙을 증명할 수 있습니다.

$$ \begin{align} \overline{a} &= \overline{c}cosB + \overline{b}cosC \\
&= \overline{c}cos90^\circ + \overline{b}cosC \\
&= \overline{c} * 0 + \overline{b}cosC \\
&= \overline{b}cosC \end{align} $$

코사인 제 1법칙 증명: 둔각 삼각형

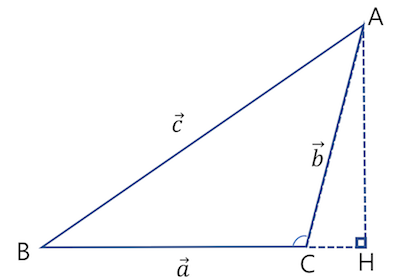
둔각 삼각형은 다음과 같이 코사인 제 1법칙을 증명할 수 있습니다.

$$ \begin{align} \overline{a} &= \overline{BH} - \overline{CH} \\
&= \overline{BH} - \overline{CH} \\
&= \overline{c}cosB - \overline{b}cos(180-C) \\
&= \overline{c}cosB - \overline{b}(-cosC) \\
&= \overline{c}cosB + \overline{b}cosC
\end{align} $$

위에서 cos은 다음과 같은 공식을 통해서 변환됩니다.

$$ cos(180-C) = -cosC $$

요약하면 코사인 제 1법칙은 다음가 같은 의미를 갖습니다.

코사인 제 2법칙

코사인 제 1법칙을 이용하여 코사인 제 2법칙을 유도할 수 있습니다.

$$ \begin{align} a^2 & = accosB + abcosC - (1)\\
b^2 & = bccosA + abcosC - (2)\\
c^2 & = bccosA + accosB - (3)\\
\end{align} $$

다음과 같이 (1)식에 (2)와 (3)식을 빼서 선분의 양쪽 각을 제거하고 대각만을 남길수 있습니다.

$$ \begin{align} a^2 - b^2 - c^2 & = accosB + abcosC - bccosA - abcosC - bccosA - accosB \\
a^2 - b^2 - c^2 & = -2bccosA \\
a^2 & = b^2 + c^2 - 2bccosA \\
\end{align} $$

이와 같이 코사인 제 2법칙을 정리할 수 있습니다.

$$ \begin{align} a^2 & = b^2 + c^2 - 2bccosA \\
b^2 & = a^2 + c^2 - 2accosB \\
c^2 & = a^2 + b^2 - 2abcosC \\
\end{align} $$

위 식은 다음과 같이 변형할 수 있습니다.

$$ \begin{align} cosA & = \frac{b^2 + c^2 - a^2}{2bc} \\
cosB & = \frac{a^2 + c^2 - b^2}{2ac} \\
cosC & = \frac{a^2 + b^2 - c^2}{2ab} \end{align} $$

벡터의 내적을 이용한 코사인 제 2법칙 증명

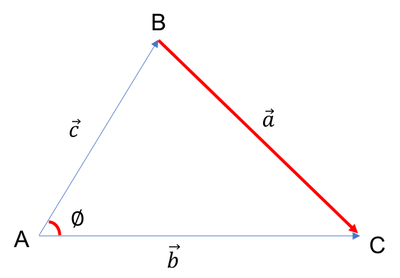
사이각을 갖는 두 벡터의 내적은 다음과 같습니다.

$$ \vec{b}\cdot\vec{c} = |\vec{b}||\vec{c}|cos\theta $$

벡터 a는 다음곽 같이 표현될 수 있으며, 다음과 같이 벡터 내적으로 코사인 제 2법칙을 증명할 수 있습니다.

$$ \begin{align} \vec{a} &= \vec{AB} - \vec{AC} = \vec{b} - \vec{c} \\
{\vec{a}}^2 &= (\vec{b} - \vec{c})^2 \\
\vec{a}\cdot\vec{a} &= \vec{b}\cdot\vec{b} -2\vec{b}\cdot\vec{c} + \vec{c}\cdot\vec{c} \\
{\overline{a}}^2 &= {\overline{b}}^2 -2|\vec{b}||\vec{c}|cos\theta + {\overline{c}}^2 \\
{\overline{a}}^2 &= {\overline{b}}^2 + {\overline{c}}^2 -2|\vec{b}||\vec{c}|cos\theta \end{align} $$