[til]처음시작하는 머신러닝 4-5장
4. 군집화
Euclidean Distance
$$ d(x, y) = \sqrt{\sum^n_{i=1}(x_i-y_i)^2} = ||X-Y|| $$
$$ Squared Euclidean Distance = \sum^n_{i=1}(x_i-y_i)^2=||X-Y||^2_2 $$
군집화 유형
- 중심기반 군집화
- k-means clustering
- k-medians clustering
- k-modes clustering
- 계층적 군집화
- 밀도기반 군집화
중심기반 군집화
- K개의 임의의 포인트 선정
- 각 데이터와 K개 포인트의 거리 계산
- 각 데이터를 K개의 포인트에 할당
- K개 포인트를 중심점으로 이동
- 2-4를 반복
계층적 군집화
- 최상의 클러스터: 모든 데이터 포함
- 최하위 클러스터: 1개의 데이터 포함
- 클러스터 방식
- 하향식 분할적 클러스터화
- 전체를 1개의 클러스터로 지정
- 중심점 지정
- 중심점에서 가장 먼 데이터 확인
- 중심점과 먼 거리 데이터를 기준으로 거리 계산
- 중심점과 먼거리에 데이터 할당
- 클러스터 별로 2-5반복
- 상향식 집괴적 클러스터화
- 1개의 1개의 클러스터로 지정
- 거리가 가까운 2개를 뭉쳐 클러스터화
- 거리가 가까운 2개 클러스터 뭉침
- 가까운 거리 기준
- 먼거리 기준
- 평균거리 기준
- 1개가 남을때 까지 반복
- 하향식 분할적 클러스터화
밀도 기반 군집화
- 유형
- 평균 이동 군집화
- DBSCAN: Density-based spatial clustering of applications with noise
- 용어
- core point: 반경 Epsilon안에 일정 개수 이상의 데이터가 존재하는 데이터
- border point: 중심 포인트보다 적지만, 중심 포인트로 부터 반경 Epsilon안에 존재하는 데이터
- noise point: core point도 border point도 아닌 데이터
- 용어
유사도 계산
- 타입
- Minkoski Distance: 벡터 공간의 두 점간 거리
- Mahalanobis distance: 점간 분포를 고려한 거리
minkowski distance
$$ d(X, Y) = \sqrt[p]{\sum^m_{i=1}|x_i-y_i|^p} $$
- p=1: Manhatan Distance
- p=2: Euclidean Distance
Mahalanobis distance:
- 공분산 이용
5장 문서 분석 시스템
- 문서 분석
- 문서 분류
- 토픽 모델링
- 문법 분석
- 단어 임베딩
문서 분류
문서 분류의 기준
- 단어 출현 빈도
- TF-IDF
- 토픽 or 클러스터링
단어 Feature: bag-of-word
- Word Frequency
- $Word\ Frequency = \frac{단어의 출현 횟수}{문서의 총 단어수}$
- Word Count
- Word Occurrence
- Word Frequency
기본 모델
- bag of words
TF-IDF
- Term Frequency Inverse-Document Frequency
- 단어 빈도 X 역문서 빈도
- $TF * \log \frac{Num\ of\ All\ Docs}{1+ Num\ Of\ Docs\ With\ Word}$
- $TF * \log [\frac{Num\ of\ All\ Docs}{1+ Num\ Of\ Docs\ With\ Word} + 1]$
- 출현 문서가 작아서 값이 급격히 커지는 현상 방지
- Smoothing IDF: Log 취하기 전에 1을 더함
- feature를 정규화하는 과정
분류 기법
- 선형회귀: 분류 확률을 출력
- SVM: 분류를 출력
- 데이타와 경계선 사이의 최소 간격을 최대화하는 경계선
- 작은 데이터에 좋은 성능 발휘
- 노이즈 영향 최소화
토픽 모델링
- 문서에 존재하는 토픽을 추출하는 기법
- 가정: 문서는 토픽으로 생성된 단어로 구성 됨
토픽
- 문서에서 발견되는 단어의 분포
- 특징
- 한개의 문서는 여러개의 토픽이 각각의 비중으로 존재
- 토픽별로 단어의 분포가 다름
- 문서 작성시 토픽의 빈중에 따라 단어로 골라 씀
토픽 모델링
- 문서가 어떤 토픽를 가질 확률
- 각 단어가 어떤 토픽에 해당할지 확률
- 토픽에 따라서 단어가 어떤 확률로 생성될지 정의하여
- 문서를 확률 모델로 만드는 과정
토픽 정보로 문서 분류에 사용

문법 분석
- 단어 중심의 분석
- 문서단위의 광의적인 해석보다는 문장단위 세부 해석에 적용
기법
- POS Tagging: Part of Speech Tagging, 품사 테깅
- NER: Named Entity Resolution, 고유명사 추출
- 단어가 어떤 의미에 포함되는지 파악
- 문장중에서 단어 추출에 이용
- 챗봇의 학습에 유용할 듯
RNN의 한계: 멀리 떨어진 연관관계를 모델링하기 어려움
LSTM: Long Short-Term Memory
- 멀리 떨어진 연관관계 모델링 탁월
단어 임베딩: Word2vec
- 단어의 의미를 나타내는 방법
- 이산표현: Discrete representation
- 호랑이: (0,0,0,0,1,0,1,….,0)
- 벡터의 길이: 어휘집 크기
- 분산표현: Distributed Representation
- 호랑이: (1.281, -2.321, …. 3.212)
- 벡터의 길이는 사용자가 지정
- 이산표현: Discrete representation
Word2vec은 분산 표현을 학습하는 모델
Word2vec
- 뉴럴넷을 이용하여 분산 표현을 학습하는 모델
- 주어진 단어와 주변 단어가 같이 일어날 확률을 구함
- 목적함수: Skip-gram, COW
Skip-gram
- 단어 하나를 받아서 그 주변에 같이 나타날 확률이 높은 단어들(context)을 구함
- 단어 하나를 받아서 그 주변에 같이 나타날 확률이 높은 단어들(context)을 구함
- $w_t$:현재 단어
- $w_{t+j}$: 윈도우 사이의 단어
- 2m+1: 윈도우 크기
- 음의 로그 손실함수
$$ p(w_0|wj)=\frac{e^{u_0^Tv_i}}{\sum_w e^{u_w^Tv_i}} $$
- COW(Continuous bag of words)
- 주변 단어(context)를 받아서 그 단어들과 같이 나나탈 확률이 높은 단어를 구함
- p(xt|context)
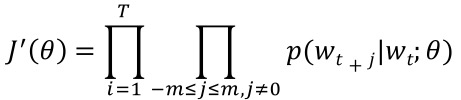
)
