2장. 주요 개념

• Topic
  • Model
  • Loss Function
  • Optimization
  • Model Evaluation

Model

• 모델이란 데이터에 대한 가정(Hypothesis)의 총합

  • 통계학에서는 Hypothesis를 Belief라고 함

• 단순(간단) 모델

  • 데이터의 단순성을 가정
  • 이해하기 쉬운 결과
  • 학습 용이
  • 복잡한 데이터를 학습하기 어려움(표현력 제약)

• 복잡한 모델

  • 가정이 없음
  • 이해하기 어려운 결과
  • 학습이 복잡
  • 새로운 데이터에 대한 성능이 떨어짐

• 결정 트리

  • 트리의 분기마다 1가지 조건으로 분기
  • 마지막 리프노드에 결과 하당

구조적 모델

• 순차모델
  • Sequence Model
    • RNN: Recurrent neural net, 순환신경망
      • 수식: $h_t = w_0 + w1h(t-1) + w_2x_t $
    • CRF: Conditional Random Field, 조건부 랜덤 필드
• 그래프모델
  • Markov Random Field
    • 문서의 문법구조
    • 이미지 픽셀 사이의 관계를 그래프로 표현

좋은 모델?

• 데이터의 패턴을 잘 학습하는 모델

• 편향/분산의 균형

  • 편향(bias)
    • 지도학습 알고리즘이 학습데이터의 입력변수들과 출력변수의 관계를 잘 학습하지 못해서 발생하는 오차
  • 분산(variance)
    • 학습 데이터의 변동성에 발생하는 오차
    • 데이터 분할
    • 학습 시점
  • 참고: http://scott.fortmann-roe.com/docs/BiasVariance.html

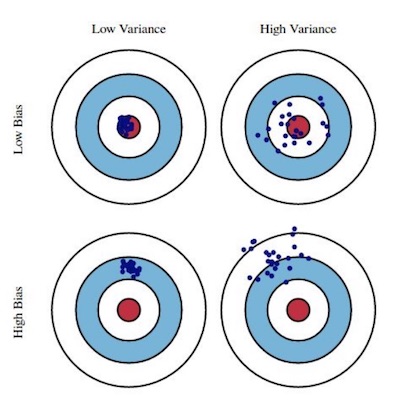
• 편향/분산 관계

  • $E[(y-\hat{f(x)})^2]=Bias[\hat{f(x)}]^2+Var[\hat{f(x)}]+\sigma^2 $
    • 오차는 편차와 분산에서 발생
    • 모델 개선을 위해서는 편차혹은 분산을 줄여야 함
  • $Bias[\hat{f(x)}]=E[\hat{f(x)}]-f(x)$
    • 편차는 학습한 모델의 예측과 이상적 모델 결과의 차이
  • $Var[\hat{f(x)}]=E[(\hat{f(x)}-E[\hat{f(x)}])^2$
    • 모델이 복잡할 수록 분산이 커짐

• 규제: Regularization

  • 가중치를 자게 만드는 기법
    • L1 Regularization
      • 불필요한 Feature 제거
      • 가중치 zero
    • L2 Regularization
      • 가중치 크기 줄임

Loss Function

• 산술 손실함수
• 확률 손실함수
  • MLE(Maximum likelyhood estimation)
  • KL-divergence
    • Kullback Leibler Divergence

• 랭킹 손실함수

  • pairwise zero-one loss: 페이와이즈 제로-원 손실함수
    • data
      • x3>x1>x2>x4>x5
        • x3>x1
        • x3>x2
        • x3>x4
        • x3>x5
        • x1>x2
        • x1>x4
        • x1>x4
        • x2>x5
        • x2>x4
        • x4>x5
      • Label: x1>x2>x3>x4>x5
      • 10중에서 8개 만족
      • 손실함수: 2
        • 만족하지 않는 대상

  • Edit Distance

    • x3>x1>x2>x4>x5
    • x1>x2>x3>x4>x5
    • edit diatance: 2 (chanage, change)

  • edit distance: 편집거리

• 모델 복잡도와 관련된 손실함수

Optimization

• 경사하강법
• 확률적 경사 하강법
• 뉴턴/준 뉴턴 방법
  • Learning Rate: %\theta := \theta - \frac{loss’(\theta)}{loss”(\theta)}%
  • 학습률 대신에 이차 미분과 이차 미분의 비율 사용
  • 장점: 경사하강법에 비하여 빠름
  • 단점: 이차 미분을 구하기 어려움, 연산비용 고가
  • 데이터가 작은 경우에 적합

• 최신 최적화 기법

  • adam: Adaptive Moment Estimation
  • AdamGrad: Adaptive Gradient

  • 주로 adam을 사용

    Evalutation

• K겹 교차검증

  • 데이터 셋을 K개로 구분
  • 첫번째 셋을 제외하고 학습, 첫번째 셋으로 평가
  • 두번째 셋을 제외하고 학습, 두번째 셋으로 평가
  • 마지막까지 반복
  • 각 셋에 대해 평가의 평균을 구함

• 평가시 고려사항

  • 데이터 항목이 한쪽으로 치우쳐 있는 경우
  • 한 분류가 다른 분류보다 중요한 경우

• 모델 평가

  • 정확도: 전제에서 대해 정확한 판정 비율
  • 재연율: 실제 양성중 양성 판정 비율
  • 정밀도: 양성 판정중 진짜 양성 비율
  • F1: 재연율과 정밀도의 조화 평균

• 랭킹평가

  • 정밀도@K: K번째 까지 정밀도
  • NDCG: 상쉬랭킹에 가산점 부여

3장. Data

데이터 유형

• Text Data

  • 의미 단위 구분 용이
  • 단어간 관계 및 문법 유추
  • 단어의 유형 다양
  • 문서를 표현할 때, Sparse Vector
  • Sequence Model 사용

• Numberic data

  • 텍스트에 비해 데이터 밀도 높음

• Image Data

  • 근접 Pixel의 연관 고려
  • 동영상의 경우 시간 근접도 고려해야 함

• 음성 데이터

  • 노이즈가 큼
  • 시간에 따른 변화 큼
  • 전처리 필요: 소리의 높낮이 및 음색 신호 처리

• Composite Data

  • 비디오(이미지, 음성) + 자막

데이터 품질

• 데이터의 레이블을 얻기 어려운 경우
  • Active Learning: 불확실성이 높은 샘플에 대하여 질의 및 결과 확인
• 특정 레이블이 부족한 경우
  • Data 분포를 균등하게 샘플링
  • 소량 데이터 학습 기법 사용: One-Shot Learning
  • Zero-shot Learning
    • 새로운 라벨이 지속적으로 생성되는 분야
• 데이터 노이즈 큼
  • 간단한 모델 사용
• 일정하지 않는 레이블
  • 클라우드 소싱으로 레이블 생성
  • 기준이 다름
  • Standization으로 전처리

데이터 표준화

Z-점수 표준화

$$ z=\frac{x-\mu}{\sigma} $$

• x: 수치값
• $\mu$: 평균
• $\sigma$: 표준편차

척도화

$$ x’=\frac{x-min(x)}{max(x)-min(x)} $$

벡터 정규화

$$ \begin{align} ||x||_2 &= \sqrt{x^2_1 + x^2_2 + …. + x^2_n} \\
&= \sqrt{\sum^n x^2_n} \\
\end{align} $$

$$ x’ = \frac{x}{||x||_2} $$

카테고리 데이터 표준화

• One-hot Encoding

서수 데이터 표준화

• 순서가 있는 카테고리
  • 별점
  • 설문: 점수

$$ \frac{t-0.5}{m} $$

• t: 점수
• m: 카테고리 수

문제 유형

• 회귀
  • 선형회귀
  • 가우시안 프로세스 회귀
  • 칼만 필터
• 분류
  • Multi-class
  • Multi-label
  • 기법
    • Logistics Regression
    • SVM
• 클러스터링
  • 데이터의 내재된 특성 분류
  • 문서: 토픽 모델링
  • 데이터의 유사도를 어떻게 판별할 것인가?
    • K-means
    • Mean Shift
• Imbedding 학습
  • 실제 Feature보다 간단
  • 기법
    • Word2vec
    • 행렬 분해