tanh 미분 정리
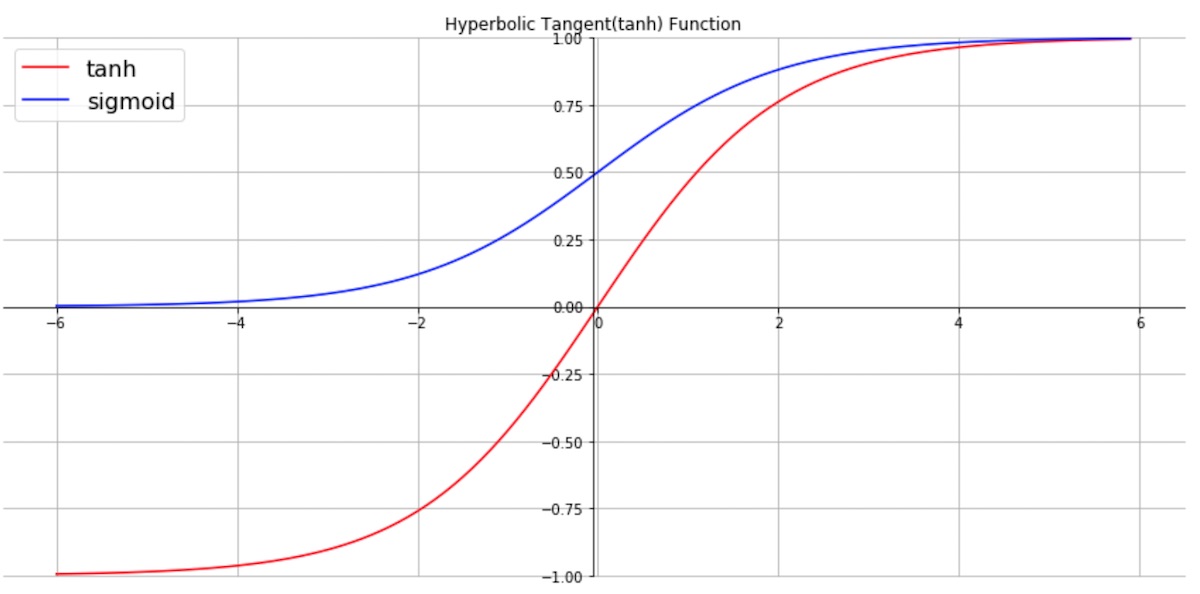
Hyperbolic Tangent(tanh) 함수는 Sigmoid의 대체제로 사용될 수 있는 활성화 함수입니다. Hyperbolic Tangent(tanh)는 Sigmoid와 매우 유사합니다. 실제로, Hyperbolic Tangent 함수는 확장 된 시그모이드 함수입니다. tanh와 Sigmoid의 차이점은 Sigmoid의 출력 범위가 0에서 1 사이인 반면 tanh와 출력 범위는 -1에서 1사이라는 점입니다. Sigmoid와 비교하여 tanh와는 출력 범위가 더 넓고 경사면이 큰 범위가 더 크기 때문에 더 빠르게 수렴하여 학습하는 특성이 있습니다.
Sigmoid와 비교하여 중심점이 0이고 범위가 기울기 넓은 차이점이 있지만 Sigmoid의 치명적인 단점인 Vanishing gradient problem 문제를 그대로 갖고 있습니다.
아래에서 tanh 함수의 실체와 미분 유도 과정을 살펴보겠습니다.
Hyperbolic Tangent(tanh) 함수 정의
Hyperbolic Tangent(tanh) 함수는 다음과 같이 정의 됩니다.
$$
\begin{align}
tanh(x) & = \frac{1-e^{-x}}{1+e^{-x}} \\
& = \frac{2}{1+e^{-2x}} -1
\end{align}
$$
Hyperbolic Tangent(tanh)은 Sigmoid와 유사한 특징을 갖습니다. Sigmoid 형태로 표현할 수 있습니다.
$$
\begin{align}
sigmoid(x) & = \frac{1}{1+e^{-x}} \\
tanh(x) & = 2sigmoid(2x) -1
\end{align}
$$
Hyperbolic Tangent 함수 미분
Hyperbolic Tangent(tanh)이 딥러닝 신경망 네트워크에 활성 함수로 사용할 경우 경사 하강법(Gradient Descent Algorithm) 계산 혹은 역전파 계산 과정에서 Hyperbolic Tangent(tanh) 함수의 미분이 사용됩니다. 이런 과정의 이해를 돕는 목적으로 tanh의 미분 과정을 정리합니다.
Hyperbolic Tangent 미분 과정
tanh 함수 미분에 사용될 미분 공식을 먼저 정리합니다.
- 주요 미분 공식 $$ \begin{align} (e^{x})’ &= e^{x} \\
(e^{-x})’ &= -e^{-x} \\
\big[ \frac{f(x)}{g(x)}\big]’ & = \frac{f’(x)g(x)-f(x)g’(x)}{g^2(x)} \end{align} $$
tanh 함수 미분 절차는 다음과 같습니다.
$$ \begin{align} f(x) & = e^{x}-e^{-x} \\
g(x) & = e^{x}+e^{-x} \\
\frac{d}{dx}tanh(x) & = \big[\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\big]’ \\
& = \big[\frac{f(x)}{g(x)}\big]’ \\
& = \frac{f’(x)g(x)-f(x)g’(x)}{g^2(x)} \\
& = \frac{(e^{x}-(-e^{-x}))(e^{x}+e^{-x}) - (e^{x}-e^{-x})(e^{x}-e^{-x} )}{(1+e^{-x})^2} \\
& = \frac{(e^{x}+e^{-x})^2 - (e^{x}-e^{-x})^2}{(e^{x}+e^{-x})^2} \\
& = \frac{(e^{x}+e^{-x})^2}{(e^{x}+e^{-x})^2} - \frac{(e^{x}-e^{-x})^2}{(e^{x}+e^{-x})^2} \\
& = 1 - \big[\frac{(e^{x}-e^{-x})}{(e^{x}+e^{-x})}\big]^2 \\
& = 1 - tanh^2(x) \\
& = (1 - tanh(x))(1 + tanh(x)) \end{align} $$
tanh 미분 결과
sigmoid의 미분 결과(도함수)는 다음과 같습니다. 앞에서 언급한 것처럼 sigmoid의 미분 결과는 매우 간결한 것 을 확인할 수 있습니다.
$$ \begin{align} \frac{d}{dx}tanh(x) & = 1- tanh^2(x) \\
& = (1-tanh(x))(1+tanh(x)) \\
\end{align} $$
다음은 sigmoid 미분결과(도함수)로 그래프를 그린 결과입니다.
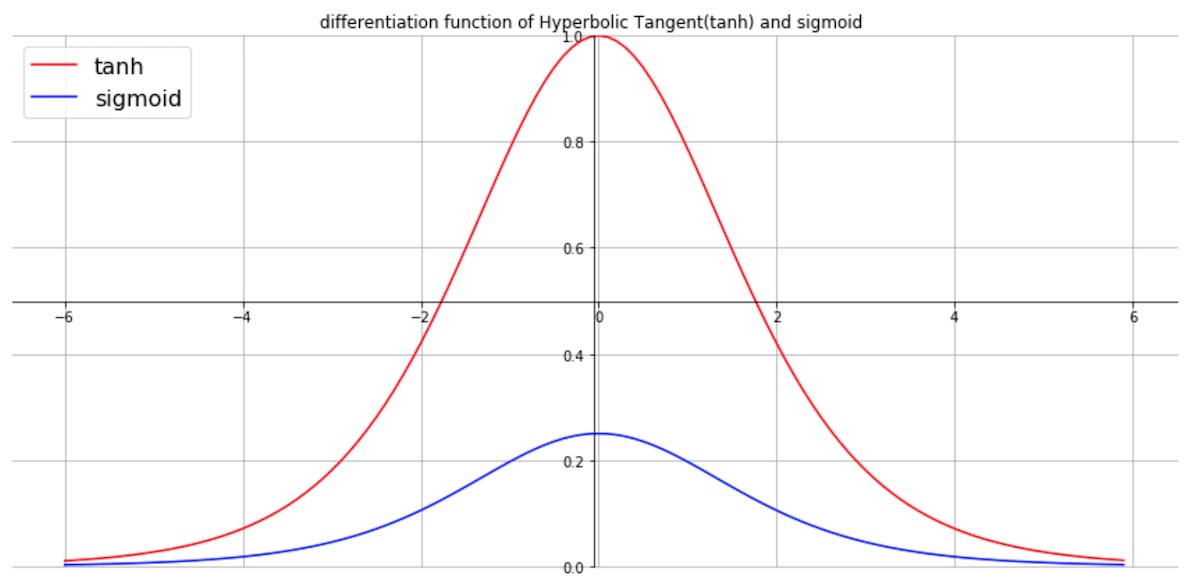
tanh 그래프의 미분계수를 보면 최댓값은 1입니다. sigmoid 미분계수와 비교하여 최대값이 4배가 큰것을 확인할 수 있습니다. sigmoid 보다는 양호하지만 tanh를 활성 함수로 사용하는 경우 은닉층의 깊이가 깊다면, tanh 역시 “vanishing gradient problem” 즉 오차율 계산이 어려운 문제가 발생할 수 있습니다. “vanishing gradient problem“이 발생하면 신경망은 더 이상의 학습이 어려워집니다.
함수 구현
파이썬으로 tanh 함수와 tanh 미분 함수는 다음과 같이 구현할 수 있습니다.
import numpy as np
def tanh(x, diff=False):
if diff:
return (1+tanh(x))*(1-tanh(x))
else:
return np.tanh(x)
