함수 표기법: 세미콜론으로 변수와 파라미터 구분

수학에서 함수를 표현하는 여러 방법이 있습니다. $f(x)$, $f\colon X\to Y$와 ${\displaystyle x\mapsto f(x).}$와 같은 방식으로 함수를 표현합니다. 복잡한 수식에서 함수를 단순하게 표기함으로써 수식을 단순하게 유지할 수 있습니다. 최근에 “딥 러닝 제대로 시작하기[↗NW] ” 책에서 약간 다른 표기법을 발견하고 그 의미를 획인해 보았습니다. “딥 러닝 제대로 시작하기[↗NW] ” 2장에서는 우도함수를 다음과 같이 표기합니다.
$$
L(w) \equiv \prod_{n=1}^{N}p(d_n|x_n;w) = \prod_{n=1}^{N}\{y(x_n;w)\}^{d_n}\{1-y(x_n;w)\}^{1-d_n}
$$
위 수식에서 조건부 확률과 출력 함수를 다음과 같이 표현하고 있습니다.
$$p(d_n|x_n;w)$$ $$y(x_n;w)$$
위 수식에서 입력 변수는 세미콜론으로 구분됩니다. 세미콜론을 포함는 함수 표현의 기본 형식은 다음과 같습니다.
$$ functionname(variables;parameters) $$
위 함수 표현 형식은 파라미터 목록으로 새로운 함수를 만들고, 변수 목록을 전달인자(Argument)로하여 함수를 호촐하는 형태로 사용됩니다. 이와 같이 세미콜론으로 변수와 파라미터를 구분함으로써 함수의 재사용성을 높이는 추상화된 개념을 표현할 수 있습니다.
$$ f(x1,x2,…;p1,p2,…) = f1(x1,x2,…) $$
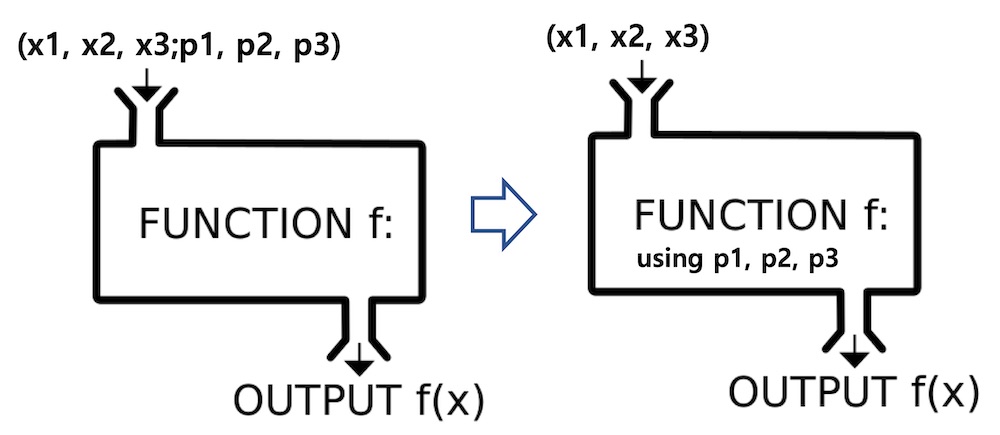
위 식에서 f함수는 p1, p2 등 파라미터 목록으로 내부 함수의 파라미터 값로 사용하여 f1을 만듭니다. 그리고 f1 함수에 x1, x2 등 변수 목록을 입력값으로 출력값을 계산합니다. 이 과정을 다음 그림과 같이 표현할 수 있습니다.
$$
L(w) \equiv \prod_{n=1}^{N}\{y(x_n;w)\}^{d_n}\{1-y(x_n;w)\}^{1-d_n}
$$
위 수식은 학습 과정에서 업데이트되는 W(가중치)를 파라미터로 전달하고 입력 데이터를 x로 하여 출력을 계산하는 함수입니다.
요약
함수의 입력 파라미터 목록에 사용되는 세미콜론은 변수와 파라미터를 구분하는 역할을 합니다. 세미콜론을 기준으로 앞은 입력 데이터인 변수이며 뒤쪽은 함수 내부에서 사용하는 파라미터입니다. 이렇게 함수 표현에 세미콜론을 사용하여 입력 데이터와 내부 파라미터를 구분할 수 있습니다. 입력을 변수와 파라미터로 구분하여 함수를 추상화하고 재사용성을 높이는 표기법입니다.